链表中，环的入口节点

给定一个链表的头节点 head ，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

不允许修改 链表。

示例 1：

输入： head = [3,2,0,-4], pos = 1 输出： 返回索引为 1 的链表节点 解释： 链表中有一个环，其尾部连接到第二个节点。

示例 2：

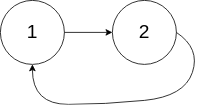
**输入：**head = [1,2], pos = 0

**输出：**返回索引为 0 的链表节点

**解释：**链表中有一个环，其尾部连接到第一个节点。

示例 3：

输入： head = [1], pos = -1

输出： 返回 null

解释： 链表中没有环。

提示：

• 链表中节点的数目范围在范围 [0, 104] 内
• -105 <= Node.val <= 105
• pos 的值为 -1 或者链表中的一个有效索引

进阶： 你是否可以使用 O(1) 空间解决此题？

/**
 * Definition for singly-linked list.
 * function ListNode(val) {
 *     this.val = val;
 *     this.next = null;
 * }
 */

/**
 * @param {ListNode} head
 * @return {ListNode}
 */
var detectCycle = function(head) {
    
};

解题思路：

• 使用快慢指针，每次快指针走两步，慢指针走一步。
• 假设表头到入环点是距离为 D，D 到第一次快慢指针相遇的点为 S1 ，S1 到入环点距离为 S2
• 到第一次相遇点，慢指针走的距离为 D + S1；快指针走的距离为 D + S1 + S2 + S1
• 快指针走的距离是慢指针的两倍，所以 2 * (D + S1) = D + S1 + S2 + S1，得出：D = S2
• 所以，两个点分别从表头和第一次相遇点出发，每次走一步，相遇的地方就是入环点

示例代码

var detectCycle = function(head) {

    // 找出第一次相遇的点
    let fast = head, slow = head, fistMeet = null
    while(slow && fast && fast.next) {
        slow = slow.next
        fast = fast.next.next
        if(slow === fast) {
            fistMeet = slow
            break
        }
    }

    if(!fistMeet) {
        return null
    }

    while(fistMeet && head) {
        if(fistMeet === head) {
            return head
        }
        fistMeet = fistMeet.next
        head = head.next
    }
    return null
}